Step 1: Variables as boxes¶

1.1 What is a variable?¶

Let’s jump right in, but what is a variable? In a programming books, variables are described as shown in the image shown in Figure 1-1.

Figure 1-1 Examples of Variable Descriptions

As shown in Figure 1-1, there is a picture of data in a box, followed by an explanation that the box is a variable. This description of the variable as a “box” nicely illustrates (to some extent) the nature of the variable. To sum up the point.

• The box and the data are two different things.

• The box contains the data (= substitution)

• Look inside the box and you’ll see the data (= reference)

You can say something like this. Let’s implement DeZero’s variables to match the image of this “box”.

1.2 Variable class implementation¶

Let’s implement the variable of DeZero as a Variable class. Incidentally, a common coding rule in Python is to capitalize the first letter of a class name. This is stated in a Python coding convention called PEP8.

Now, let’s implement the Variable class as a “box”. If we were to write that function with minimal code, it would look something like this

[1]:

class Variable:
    def __init__(self, data):
        self.data = data

As you can see, we just need to set the arguments given in the initialization to the instance variable data. It’s very simple code, but you can now use the Variable class as a “box”. This is because the actual data is stored in the data of the Variable. This will become clearer if you look at the following use case.

[2]:

import numpy as np

data = np.array(1.0)
x = Variable(data)
print(x.data)

1.0

In this example, we use “NumPy’s multidimensional array” as the data to be placed in the box. In this case, x is a Variable instance, and the actual data is in x. In other words, x is not data, but a being that has data - a box that holds data.

We then try to assign the new data to x in the code above. It can be written in the following way:

[3]:

x.data = np.array(2.0)
print(x.data)

2.0

As shown here, the new data is assigned by writing x.data = np.array(2.0). Now the Variable class can be used as a “box”.

That’s all of the implementation we’ll be doing in this step. Currently, the Variable class has only three lines of code, but we’ll use this as a starting point to build DeZero into a modern framework.

1.3 [Supplement] NumPy’s multidimensional array¶

Finally, we will briefly supplement NumPy’s multidimensional array. A multidimensional array is a data structure in which elements, such as numbers, are gathered in regular rows. A sequence of elements has a “direction”, which is called a “dimension” or “axis”. Figure 1-2 shows an example of a multidimensional array.

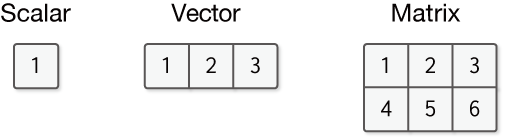
Figure 1-2 Example of a multidimensional array

Figure 1-2 shows the 0-dimensional array, the 1-dimensional array, and the 2-dimensional array, in order from left to right. They are called scalars, vectors, and matrices. A scalar simply represents a single number. Vectors are numbers along one axis, and matrices are numbers along two axes.

The ndarray instance of NumPy has an instance variable called ndim. ndim is an abbreviation of “number of dimensions”, which means the “number of dimensions” of a multi-dimensional array. In practice, it looks like this:

[4]:

import numpy as np

x = np.array(1)
print(x.ndim)

x = np.array([1, 2, 3])
print(x.ndim)

x = np.array([[1, 2, 3], [4, 5, 6]])
print(x.ndim)

0
1
2

As shown above, the instance variable ndim gives us the number of dimensions.