ステップ1 箱としての変数¶

1.1 変数とは¶

早速ですが、変数とは何でしょうか？ プログラミングの入門書などを開くと、変数は、おおよそ図1-1のようなイメージで説明されます。

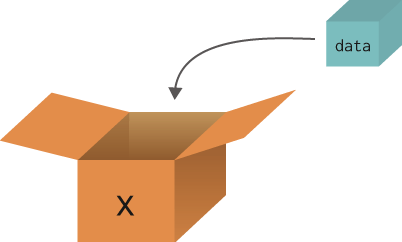
図1-1 変数の説明例

図1-1のように、箱にデータを入れる絵があり、その箱が変数であるという説明が続きます。この変数を「箱」にたとえた説明は、変数の性質を（ある程度は）上手く表しています。要点をまとめると、

• 箱とデータは別物である

• 箱にはデータが入る（= 代入）

• 箱の中を覗けばデータが分かる（= 参照）

といったことが言えるでしょう。それでは、この「箱」のイメージに合うように、DeZeroの変数を実装してみましょう。

1.2 Variableクラスの実装¶

変数は英語でvariableです。そこで、DeZeroの変数をVariableクラスとして実装することにします。ちなみにPythonでは、クラス名の頭文字を大文字にするのが一般的なコーディング規則です。このことは、PEP8というPythonのコーディング規約で述べられています。

それでは、Variableクラスが「箱」となるように実装してみましょう。その機能を最小限のコードで書くとすれば、次のようになります。

[1]:

class Variable:
    def __init__(self, data):
        self.data = data

見てのとおり、初期化で与えられた引数をインスタンス変数のdataに設定するだけです。とても単純なコードですが、これでVariableクラスは「箱」として使うことができます。なぜなら、実際のデータはVariableのdataに保持されるからです。これは次の使用例を見ると、より明確になるでしょう。

[2]:

import numpy as np

data = np.array(1.0)
x = Variable(data)
print(x.data)

1.0

この例では、箱に入れるデータとして「NumPyの多次元配列」を用いています。このとき、xはVariableインスタンスであり、実際のデータはxの中にあります。つまり、xはデータではなく、データを持つ存在――データを詰める箱――というわけです。

続いて、上のコードのxに新しいデータを代入してみます。それには、次のように書くことができます。

[3]:

x.data = np.array(2.0)
print(x.data)

2.0

ここで示したように、x.data = ...と書けば、新しいデータが代入されます。これで、Variableクラスは「箱」として使えるようになりました。

以上が本ステップで行う実装のすべてです。現在、Variableクラスにはわずか3行のコードしかありませんが、ここを出発点として、DeZeroをモダンなフレームワークへと作り上げていきます。

1.3 【補足】NumPyの多次元配列¶

最後に、NumPyの多次元配列について簡単に補足します。多次元配列とは、数値などの要素が規則的に並んで集まったデータ構造です。要素の並びには“方向”があり、その方向は「次元」や「軸」と呼ばれます。図1-2に多次元配列の例を示します。

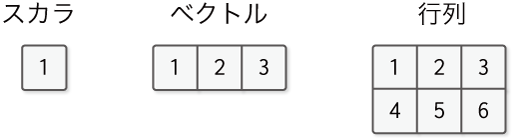
図1-2 多次元配列の例

図1-2は、左から順に、0次元配列、1次元配列、2次元配列です。それらはスカラ、ベクトル、行列と呼ばれます。スカラは単に1つの数を表します。ベクトルは1つの軸に沿って数が並び、行列は2つの軸に沿って数が並びます。

NumPyのndarrayインスタンスには、ndimというインスタンス変数があります。ndimとは、number of dimensionsの略で、多次元配列の「次元の数」を意味します。実際に使ってみると、次のようになります。

[4]:

import numpy as np

x = np.array(1)
print(x.ndim)

x = np.array([1, 2, 3])
print(x.ndim)

x = np.array([[1, 2, 3], [4, 5, 6]])
print(x.ndim)

0
1
2

上記のように、インスタンス変数のndimによって、次元の数が分かります。